Funções do 1º e 2º graus

Funções do 1º e 2º graus

Função do 1º grau

É uma função de IR em IR, ou seja, pertence ao conjunto dos números reais
f(x) = ax + b ou y= ax + b
Onde a é o coeficiente de x e b é o termo constante.
Regra: a e b são números reais e a≠0

Se preferir o vídeo abaixo tem a postagem em vídeo e áudio:

Ex.: f(x) = 8x – 3 onde a = 8 e b = -3

f(x) = 5x onde a = 5 e b = 0



Construção do gráfico:


O gráfico é sempre uma reta.

Para construir um gráfico é necessário dois pares ordenados de pontos que pertençam a esta reta.

Depois colocamos no plano cartesiano e traçamos uma reta.

Então vamos fazer a função abaixo:

y = 3x -2

1º temos que encontras os pares ordenados e para isso escolhemos aleatoriamente dois valores para o x e assim construirmos o gráfico.

Vamos escolher x=1 e x=2

Para x = 1 teremos: y = 3x – 2 → y = 3 (1) – 2 → y = 3 – 2 → y = 1 par ordenado (1,1)

Para x =   2 teremos:  y = 3x – 2  → y = 3 (2) – 2 → y = 6 – 2 → y = 4 par ordenado (2,4)

Encontramos então os pares ordenado (1,1) e (2,4)

2° Colocamos estes pares ordenados no plano cartesiano e traçamos uma reta




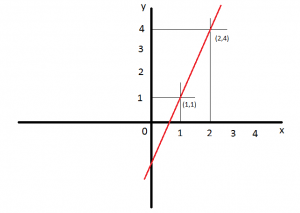
Podemos também determinar uma função de 1º grau partindo de um gráfico
Vamos a um exemplo:



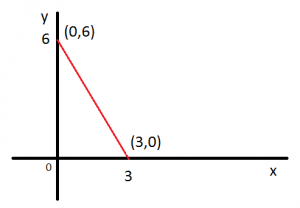
Usamos a função y = ax + b

Agora é só substituir:

(0,6) → y= ax + b → 6 = a (0) + b → b = 6

(3,0) → y= ax + b → 0 = a (3) + b → 3 a + b = 0 → 3 a = - b → 3 a = - 6 → a = - 2

Sabemos agora que a = - 2 e b = 6

Substituindo a e b fica assim a função: y = - 2 x + 6

ATENÇÃO: Resolver questões é a melhor maneira de aprender: Funções do 1º e 2º Graus - Problemas

Função do 2º Grau

Dados os números reais a, b e c (coeficientes da função), com a ≠ 0, chama-se função do 2º grau, ou função quadrática a função, definida por f(x) = ax² + bx + c  ou y = ax² + bx + c

São exemplos de funções do 2º grau:

a) f(x) = 4x² –2x – 3, em que a = 4, b = -2 e c = - 3

b) f(x) = 2x² –3x, em que a = 2, b = -3 e c = 0

c) y = -x² + 5, onde a = -1, b = 0 e c = 5

d) y = 5x², onde a = 5, b = 0 e c = 0


Gráfico da função do 2º grau


O gráfico de uma função do 2º grau é uma curva chamada parábola.







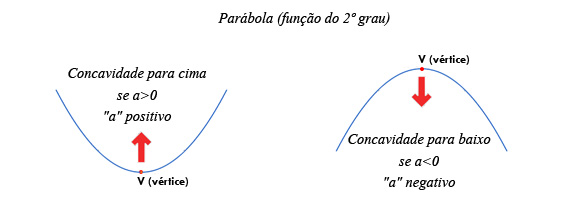
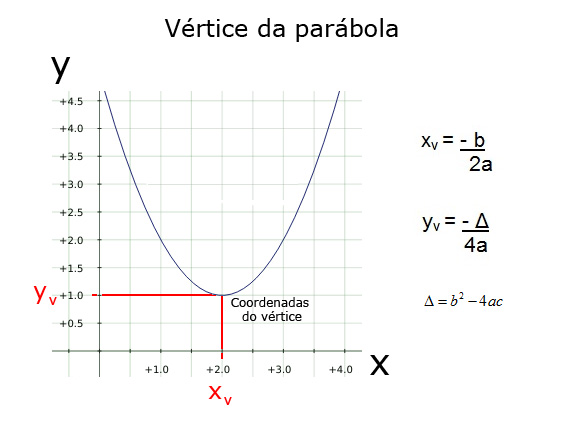
Vamos agora construir um gráfico da função de 2º grau

Exemplo: 
f(x) = 2x² + 4x - 6

f(x) = ax² + bx + c.

2x² + 4x – 6 = 0

y = 2x² + 4x – 6

ATENÇÃO: O coeficiente “c” indica o ponto de encontro de uma parábola com o eixo y

Para montar um gráfico da função de 2º grau nós devemos encontrar as coordenadas das raízes e do vértice.


1º Vamos achar as coordenadas das raízes

As raízes nos mostrarão a intersecção com o eixo x

As raízes você encontra através de uma equação de 2º grau utilizando as fórmulas de Bhaskara:



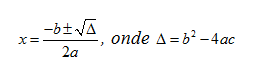
Igualamos a equação da função a zero, ficando assim:

2x² + 4x – 6 = 0

Primeiro encontramos o delta:

Sabemos que a= 2, b= 4 e c= -6


∆ = (4)² – 4.2. (– 6)

∆ = 16 – 8.(– 6)

∆ = 16 + 48

∆ = 64

Vamos encontrar as coordenadas das raízes:

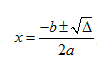
Sabemos que a= 2, b= 4 e c= -6



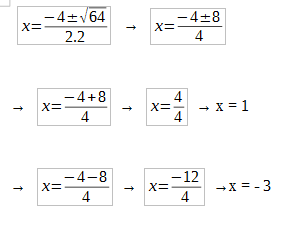
Bom achamos as coordenadas x = 1 e -3

Vamos achar agora as coordenadas dos y

Para x = 1 temos,

y = 2x² + 4x – 6 → y = 2.(1)² + 4(1) – 6 → y = 2.1 + 4 – 6 → y = 2 – 2

Então y = 0 primeira coordenada (1,0)


Para x = - 3 temos,

y = 2x² + 4x – 6 → y = 2.(-3)² + 4(-3) – 6 → y = 2.9 - 12 – 6 → y = 18 – 18

Então y = 0 segunda coordenada (-3,0)


As coordenadas das raízes são (1,0) e (-3,0)


2º Devemos agora encontrar o vértice



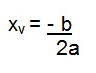
Xv = -4/2.2 → -4/4   → Xv = -1



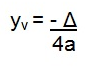
Yv = -64/ 4.2 → -64/ 8 → Yv = -8


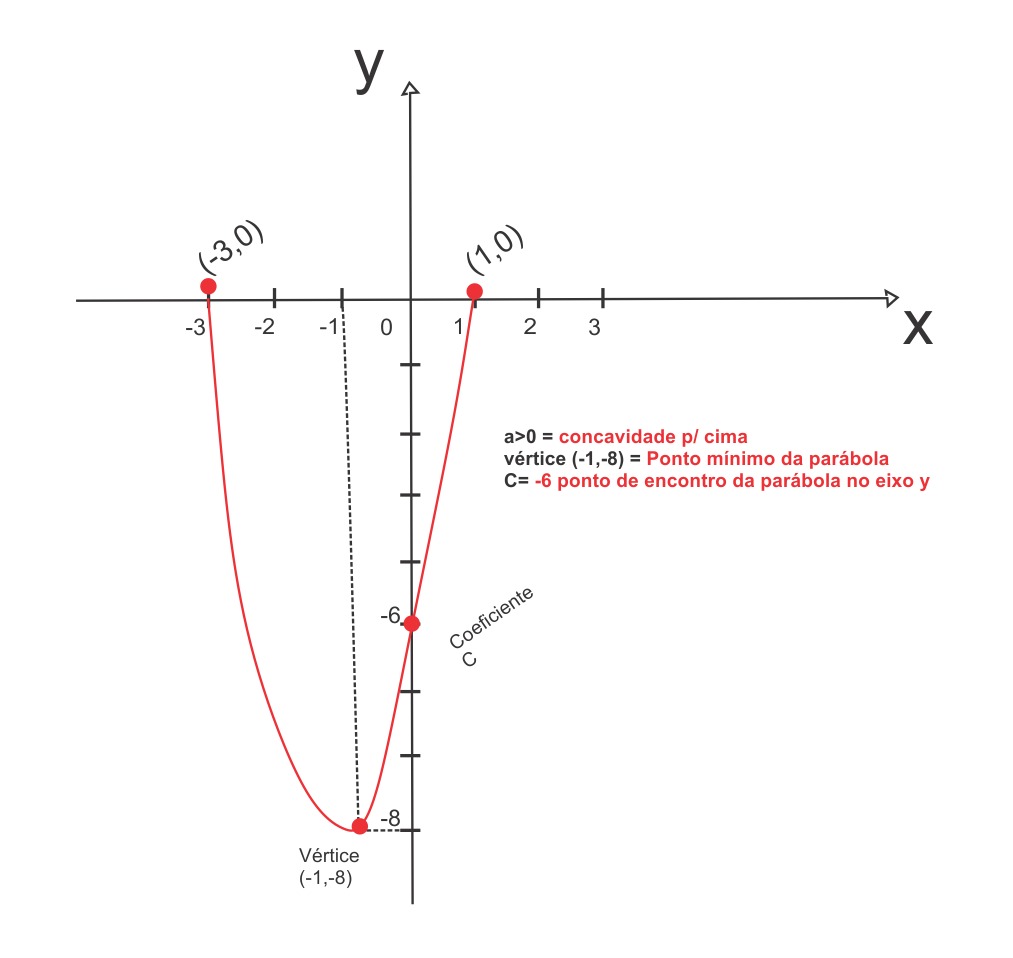
As coordenadas do vértice é (-1, -8)


O que sabemos:

a > 0 então a concavidade da parábola é para cima

c = -6 então a parábola passará em -6 no eixo y

Vértice (-1,-8) Esta é a coordenada mais baixa da parábola

As coordenadas das raízes são (1,0) e (-3,0)

Agora fica fácil construirmos o gráfico:



Podemos também determinar uma função de 2º grau partindo de um gráfico

O processo é o mesmo da função do 1º grau, usando agora a fórmula do 2º grau

f(x) = ax² + bx + c ou y = ax² + bx + c

No gráfico temos:

As coordenadas das raízes são (1,0) e (-3,0)

Coeficiente c = -6

Agora podemos achar os coeficientes “a” e “b” através da fórmula do 2º grau

Vamos lá então:

Coordenadas (1,0)
y = ax² + bx + c
0 = a(1)² + b (1) -6
a +b -6 = 0
b = 6 – a

Coordenadas (-3,0)
y = ax² + bx + c
0 = a(-3)² + b (-3) -6
9a -3b -6 = 0
9a = 3b + 6


Sabemos que b = 6 – a
Logo:

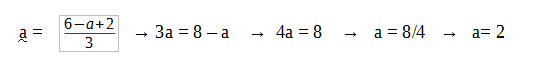
Então:

b = 6 – a → b = 6 – 2 → b = 4

Logo,

a = 2    b = 4     c = -6

Agora podemos determinar a função:

f(x) = ax² + bx + c
f(x) = 2x² + 4x - 6

ATENÇÃO: Resolver questões é a melhor maneira de aprender: Funções do 1º e 2º Graus - Problemas